Table Of Contents
- 1.2. NeXus Design
Previous topic
NAPI: The NeXus Application Programming Interface
Next topic
1.2.3.1. Rules for Structuring Information in NeXus Files
This Page
Quick search
Enter search terms or a module, class or function name.
This chapter actually defines the rules to use for writing valid NeXus files. An explanation of NeXus objects is followed by the definition of NeXus coordinate systems, the rules for structuring files and the rules for storing single items of data.
The structure of NeXus files is extremely flexible, allowing the storage both of simple data sets, such as a single data array and its axes, and also of highly complex data, such as the simulation results or an entire multi-component instrument. This flexibility is a necessity as NeXus strives to capture data from a wild variety of applications in X-ray, muSR and neutron scattering. The flexibility is achieved through a hierarchical structure, with related fields collected together into groups, making NeXus files easy to navigate, even without any documentation. NeXus files are self-describing, and should be easy to understand, at least by those familiar with the experimental technique.
Note
In this manual, we use the terms field, data field, and data item synonymously to be consistent with their meaning between NeXus data file instances and NXDL specification files.
Before discussing the design of NeXus in greater detail it is necessary to define the objects and terms used by NeXus. These are:
In the following sections these elements of NeXus files will be defined in more detail.
NeXus files consist of data groups, which contain fields and/or other groups to form a hierarchical structure. This hierarchy is designed to make it easy to navigate a NeXus file by storing related fields together. Data groups are identified both by a name, which must be unique within a particular group, and a class. There can be multiple groups with the same class but they must have different names (based on the HDF rules).
For the class names used with NeXus data groups the prefix NX is reserved. Thus all NeXus class names start with NX.
Data fields contain the essential information stored in a NeXus file. They can be scalar values or multidimensional arrays of a variety of sizes (1-byte, 2-byte, 4-byte, 8-byte) and types (integers, floats, characters). The fields may store both experimental results (counts, detector angles, etc), and other information associated with the experiment (start and end times, user names, etc). Data fields are identified by their names, which must be unique within the group in which they are stored. Some fields have engineering units to be specified. In some cases, such in NXdetector/data, a field is expected to have be an array of several dimensions.
Examples of data fields
- variable (NX_NUMBER)
- Dimension scale defining an axis of the data.
- variable_errors (NX_NUMBER)
- Errors (uncertainties) associated with axis variable.
- wavelength (NX_FLOAT)
- wavelength of radiation, units="NX_FLOAT"
- chemical_formula (NX_CHAR)
- The chemical formula specified using CIF conventions.
- name (NX_CHAR)
- Name of user responsible for this entry.
- data (NX_NUMBER)
- Data values from the detector, units="NX_ANY"
Attributes are extra (meta-)information that are associated with particular fields. They are used to annotate the data, e.g. with physical units or calibration offsets, and may be scalar numbers or character strings. In addition, NeXus uses attributes to identify plottable data and their axes, etc. A description of some of the many possible attributes can be found in the next table:
Examples of data attributes
- units (NX_CHAR)
- Data units given as character strings, must conform to the NeXus units standard. See the NeXus Data Units section for details.
- signal (NX_POSINT)
- Defines which data set contains the signal to be plotted, use signal=1 for main signal, signal=2 for a second item to plot, and so on.
- axes (NX_CHAR)
axes defines the names of the dimension scales for this data set as a colon-delimited list. Note that some legacy data files may use a comma as delimiter.
For example, suppose data is an array with elements data[j][i] (C) or data(i,j) (Fortran), with dimension scales time_of_flight[i] and polar_angle[j], then data would have an attribute axes="polar_angle:time_of_flight" in addition to an attribute signal=1.
- axis (NX_POSINT)
- The original way of designating data for plotting, now superceded by the axes attribute. This defines the rank of the signal data for which this data set is a dimension scale in order of the fastest varying index (see a longer discussion in the section on NXdata structure), i.e. if the array being stored is data, with elements data[j][i] in C and data(i,j) in Fortran, axis would have the following values: ith dimension (axis=1), jth dimension (axis=2), etc.
- primary (NX_POSINT)
- Defines the order of preference for dimension scales which apply to the same rank of signal data. Use primary=1 to indicate preferred dimension scale
- long_name (NX_CHAR)
- Defines title of signal data or axis label of dimension scale
- calibration_status (NX_CHAR)
- Defines status of data value - set to Nominal or Measured
- offset (NX_INT)
- Rank values of offsets to use for each dimension if the data is not in C storage order
- stride (NX_INT)
- Rank values of steps to use when incrementing the dimension
- vector (NX_FLOAT)
- 3 values describing the axis of rotation or the direction of translation
- interpretation (NX_CHAR)
Describes how to display the data. Allowed values include:
- scaler (0-D data)
- spectrum (1-D data)
- image (2-D data)
- vertex (3-D data)
Finally, NeXus files themselves have global attributes which are listed in the next table. These attributes identify the NeXus version, file creation time, etc. All attributes are identified by their names, which must be unique within each field.
Examples of global attributes
- file_name (NX_CHAR)
- File name of original NeXus file to assist in identification if the external name has been changed
- file_time (ISO 8601)
- Date and time of file creation
- file_update_time (ISO 8601)
- Date and time of last file change at close
- NeXus_version (NX_CHAR)
- Version of NeXus API used in writing the file
- creator (NX_CHAR)
- Facility or program where the file originated
Links are pointers to existing data somewhere else. The concept is very much like symbolic links in a unix filesystem. The NeXus definition sometimes requires to have access to the same data in different groups in the same file. For example: detector data is stored in the NXinstrument/NXdetector group but may be needed in NXdata for automatic plotting. Rather then replicating the data, NeXus uses links in such situations. See the figure for a more descriptive representation of the concept of linking.
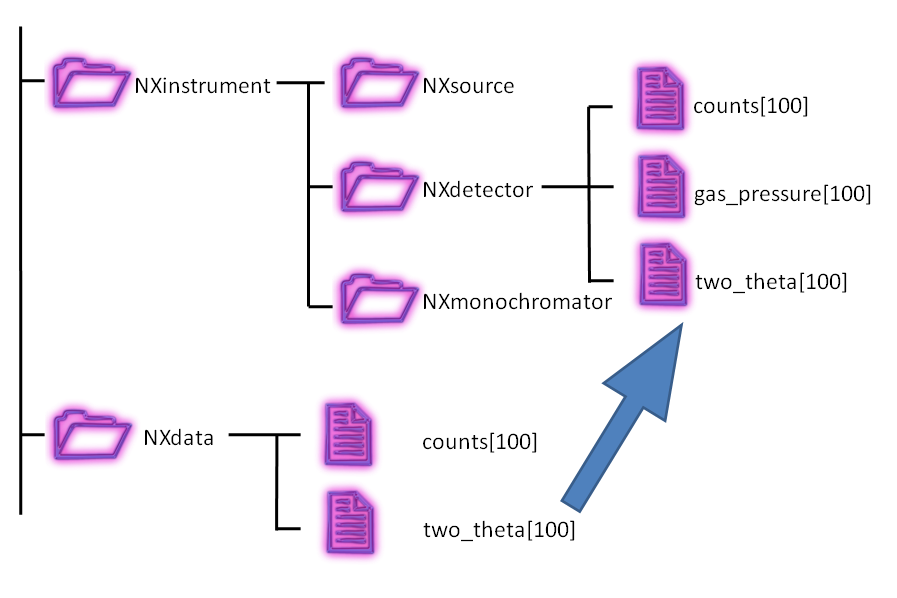
Linking in a NeXus file
NeXus also allows for links to external files. Consider the case where an instrument uses a detector with a closed-system software support provided by a commercial vendor. This system writes its images into a NeXus HDF5 file. The instrument’s data acquisition system writes instrument metadata into another NeXus HDF5 file. In this case, the instrument metadata file might link to the data in the detector image file. Here is an example (from Diamond Light Source) showing an external file link in HDF5:
Example of linking to data in an external HDF5 file
Data groups often describe objects in the experiment (monitors, detectors, monochromators, etc.), so that the contents (both data fields and/or other data groups) comprise the properties of that object. NeXus has defined a set of standard objects, or base classes, out of which a NeXus file can be constructed. This is each data group is identified by a name and a class. The group class, defines the type of object and the properties that it can contain, whereas the group name defines a unique instance of that class. These classes are defined in XML using the NeXus Definition Language (NXDL) format. All NeXus class types adopted by the NIAC must begin with NX. Classes not adopted by the NIAC must not start with NX.
Note
NeXus base classes are the components used to build the NeXus data structure.
Not all classes define physical objects. Some refer to logical groupings of experimental information, such as plottable data, sample environment logs, beam profiles, etc. There can be multiple instances of each class. On the other hand, a typical NeXus file will only contain a small subset of the possible classes.
Note
The groups, fields, links, and attributes of a base class definition are all optional, with a few particular exceptions in NXentry and NXdata. They are named in the specification to describe the exact spelling and usage of the term when it appears.
NeXus base classes are not proper classes in the same sense as used in object oriented programming languages. In fact the use of the term classes is actually misleading but has established itself during the development of NeXus. NeXus base classes are rather dictionaries of field names and their meanings which are permitted in a particular NeXus group implementing the NeXus class. This sounds complicated but becomes easy if you consider that most NeXus groups describe instrument components. Then for example, a NXmonochromator base class describes all the possible field names which NeXus allows to be used to describe a monochromator.
Most NeXus base classes represent instrument components. Some are used as containers to structure information in a file (NXentry, NXcollection, NXinstrument, NXprocess, NXparameter). But there are some base classes which have special uses which need to be mentioned here:
These groups can appear anywhere in the NeXus hierarchy, where needed. Preferably close to the component they annotate or in a NXcollection. All of the base classes are documented in the reference manual.
The most notable special base class (or group in NeXus) is NXdata. NXdata is the answer to a basic motivation of NeXus to facilitate automatic plotting of data. NXdata is designed to contain the main dataset and its associated dimension scales (axes) of a NeXus data file. The usage scenario is that an automatic data plotting program just opens a NXentry and then continues to search for any NXdata groups. These NXdata groups represent the plottable data. An algorithm for identifying the default plottable data is presented in the chapter titled Rules for Storing Data Items in NeXus Files.
There are many ways to store metadata about your experiments. Already there are many fields in the various base classes to store the more common or general metadata, such as wavelength. (For wavelength, see the Strategies: The wavelength section.)
One common scheme is to store the metadata all in one group. If the group is to be validated for content, then there are several possibilities, as shown in the next table:
| base class | intent |
|---|---|
| NXnote | to store additional information |
| NXlog | information that is time-stamped |
| NXparameters | parameters for processing or analysis |
| NXcharacterization | do not use this, as it may be removed later |
If the content of the metadata group is to be excluded from validation, then store it in a NXcollection group.
The objects described so far provide us with the means to store data from a wide variety of instruments, simulations, or processed data as resulting from data analysis. But NeXus strives to express strict standards for certain applications of NeXus, too. The tool which NeXus uses for the expression of such strict standards is the NeXus Application Definition. A NeXus Application Definition describes which groups and data items have to be present in a file in order to properly describe an application of NeXus. For example for describing a powder diffraction experiment. Typically an application definition will contain only a small subset of the many groups and fields defined in NeXus. NeXus application definitions are also expressed in the NeXus Definition Language (NXDL). A tool exists which allows one to validate a NeXus file against a given application definition.
Note
NeXus application definitions define the minimum required information necessary to satisfy data analysis or other data processing.
Another way to look at a NeXus application definition is as a contract between a file producer (writer) and a file consumer (reader).
The contract reads: If you write your files following a particular NeXus application definition, I can process these files with my software.
Yet another way to look at a NeXus application definition is to understand it as an interface definition between data files and the software which uses this file. Much like an interface in the Java or other modern object oriented programming languages.
In contrast to NeXus base classes, NeXus supports inheritance in application definitions.
Please note that a NeXus Application Definition will only define the bare minimum of data necessary to perform common analysis with data. Practical files will nearly always contain more data. One of the beauties of NeXus is that it is always possible to add more data to a file without breaking its compliance with its application definition.
The NeXus coordinate system is shown below. Note that it is the same as that used by McStas (http://mcstas.risoe.dk).
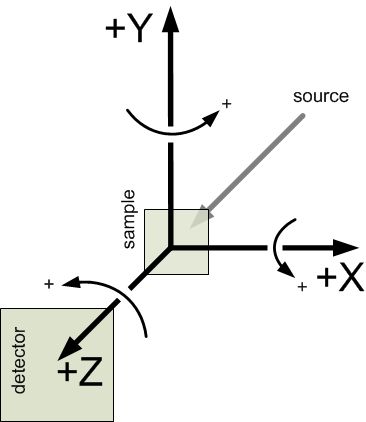
NeXus coordinate system, as viewed from detector
Note
The NeXus definition of +z is opposite to that in the IUCr International Tables for Crystallography, volume G, and consequently, +x is also reversed.
Coordinate systems in NeXus have undergone significant development. Initially, only motor positions of the relevant motors were stored without further standardization. This soon proved to be too little and the NeXus polar coordinate system was developed. This system still is very close to angles that are meaningful to an instrument scientist but allows to define general positions of components easily. Then users from the simulation community approached the NeXus team and asked for a means to store absolute coordinates. This was implemented through the use of the NXgeometry class on top of the McStas system. We soon learned that all the things we do can be expressed through the McStas coordinate system. So it became the reference coordinate system for NeXus. NXgeometry was expanded to allow the description of shapes when the demand came up. Later, members of the CIF team convinced the NeXus team of the beauty of transformation matrices and NeXus was enhanced to store the necessary information to fully map CIF concepts. Not much had to be changed though as we choose to document the existing angles in CIF terms. The CIF system allows to store arbitrary operations and nevertheless calculate absolute coordinates in the laboratory coordinate system. It also allows to convert from local, for example detector coordinate systems, to absolute coordinates in the laboratory system.
Please note that NXgeometry and the polar coordinate system are suggested to be deprecated. For new projects, rather use the CIF approach.
As stated above, NeXus uses the McStas coordinate system (http://mcstas.risoe.dk) as its laboratory coordinate system. The instrument is given a global, absolute coordinate system where the z axis points in the direction of the incident beam, the x axis is perpendicular to the beam in the horizontal plane pointing left as seen from the source, and the y axis points upwards. See below for a drawing of the McStas coordinate system. The origin of this coordinate system is the sample position or, if this is ambiguous, the center of the sample holder with all angles and translations set to zero. The McStas coordinate system is illustrated in the next figure:
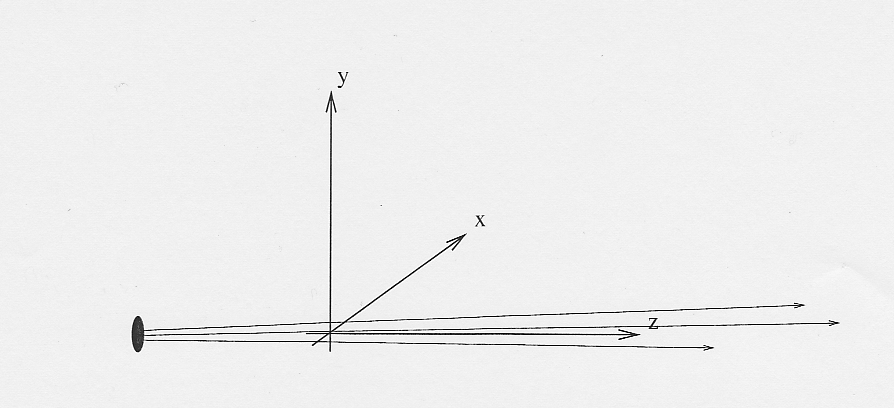
The McStas Coordinate System
The NeXus NXgeometry class directly uses the McStas coordinate system. NXgeometry classes can appear in any component in order to specify its position. The suggested name to use is geometry. In NXgeometry the NXtranslation/values field defines the absolute position of the component in the McStas coordinate system. The NXorientation/value field describes the orientation of the component as a vector of in the McStas coordinate system.
Please note that it is planned to deprecate NXgeometry in favour of the transformation based system described below.
In this system, the instrument is considered as a set of components through which the incident beam passes. The variable distance is assigned to each component and represents the effective beam flight path length between this component and the sample. A sign convention is used where negative numbers represent components pre-sample and positive numbers components post-sample. At each component there is local spherical coordinate system with the angles polar_angle and azimuthal_angle. The size of the sphere is the distance to the previous component.
In order to understand this spherical polar coordinate system it is helpful to look initially at the common condition that azimuthal_angle is zero. This corresponds to working directly in the horizontal scattering plane of the instrument. In this case polar_angle maps directly to the setting commonly known as two theta. Now, there are instruments where components live outside of the scattering plane. Most notably detectors. In order to describe such components we first apply the tilt out of the horizontal scattering plane as the azimuthal_angle. Then, in this tilted plane, we rotate to the component. The beauty of this is that polar_angle is always two theta. Which, in the case of a component out of the horizontal scattering plane, is not identical to the value read from the motor responsible for rotating the component. This situation is shown in Polar Coordinate System.
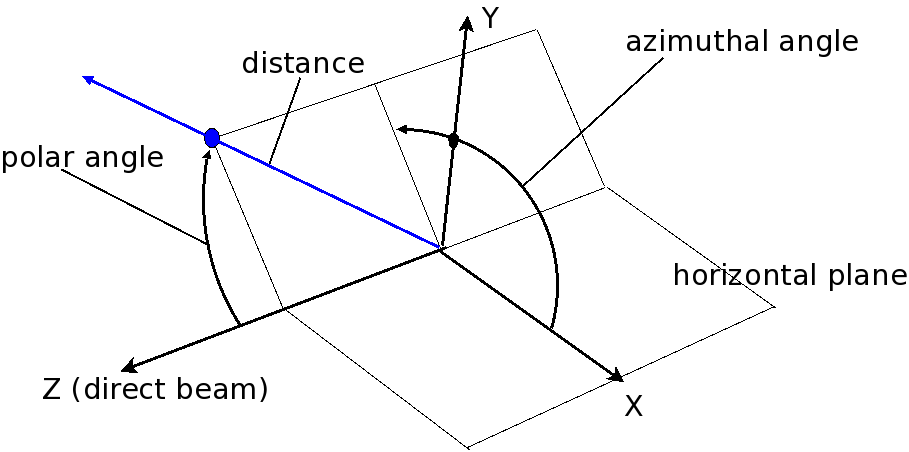
NeXus Simple (Spherical Polar) Coordinate System
Another way to look at coordinates is through the use of transformation matrices. In this world view, the absolute position of a component or a detector pixel with respect to the laboratory coordinate system is calculated by applying a series of translations and rotations. These operations are commonly expressed as transformation matrices and their combination as matrix multiplication. A very important aspect is that the order of application of the individual operations does matter. Another important aspect is that any operation transforms the whole coordinate system and gives rise to a new local coordinate system. The mathematics behind this is well known and used in such applications such as industrial robot control, space flight and computer games. The beauty in this comes from the fact that the operations to apply map easily to instrument settings and constants. It is also easy to analyze the contribution of each individual operation: this can be studied under the condition that all other operations are at a zero setting.
In order to use coordinate transformations, several morsels of information need to be known:
- Type
- The type of operation: rotation or translation
- Direction
- The direction of the translation or the direction of the rotation axis
- Value
- The angle of rotation or the length of the translation
- Order
- The order of operations to apply to move a component into its place.
NeXus chooses to encode this information in the following way:
- Type
- Through a data set attribute transformation_type. This can take the value of either translation or rotation.
- Direction
- Through a data set attribute vector. This is a set of three values describing either the components of the rotation axis or the direction along which the translation happens.
- Value
- This is represented in the actual data of the data set. In addition, there is the offset attribute which has three components describing a translation to apply before applying the operation of the real axis. Without the offset attribute additional virtual translations would need to be introduced in order to encode mechanical offsets in the axis.
- Order
The order is encoded through the depends_on attribute on a data set. The value of the depends_on attribute is the axis upon which the current axis sits. If the axis sits in the same group it is just a name, if it is in another group it is a path to the dependent axis. In addition, for each beamline component, there is a depends_on field which points to the data set at the head of the axis dependency chain. Take as an example an eulerian cradle as used on a four-circle diffractometer. Such a cradle has a dependency chain of phi:chi:rotation_angle. Then the depends_on field in NXsample would have the value phi.
NeXus Transformation encoding
Transformation encoding for an eulerian cradle on a four-circle diffractometer
The type and direction of the NeXus standard operations is documented below in the table: Actions of standard NeXus fields. The rule is to always give the attributes to make perfectly clear how the axes work. The CIF scheme also allows to store and use arbitrarily named axes in a NeXus file.
Actions of standard NeXus fields
| Field Name | transformation_type | vector |
|---|---|---|
| polar_angle | rotation | 0 1 0 |
| azimuthal_angle | rotation | 0 0 1 |
| meridional_angle | rotation | 1 0 0 |
| distance | translation | 0 0 1 |
| height | translation | 0 1 0 |
| x_translation | translation | 1 0 0 |
| chi | rotation | 0 0 1 |
| phi | rotation | 0 1 0 |
For the NeXus spherical coordinate system, the order is implicit and is given in the next example.
implicit order of NeXus spherical coordinate system
azimuthal_angle:polar_angle:distance
This is also a nice example of the application of transformation matrices: